Binary blog-post 1

Binary is the name given to numbers in base 2.  This means the only digits that can be used are 0 and 1.  We use the powers of 2 as column headings.  Here is an example:

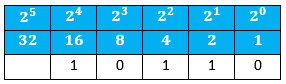
This shows 22 in binary, because 16 + 4 + 2 = 22 

How can we write 43 in binary?  Try it first before scrolling down (but it is then worth doing so, because there are at least two different ways of doing this!).

.

.

.

.

.

.

.

.

We could start at the left-hand end and see whether we need each number.

So:  the biggest power of 2 that fits in 43 is 32.  (We don’t need to worry about 64, 128, 256, etc.)

Put a 1 in the 32 column and subtract 32 from 43, leaving 11.  There are no 16s in 11, so put a zero in the 16 column.  There is an 8, so put a 1 in the 8 column and subtract that from 11 to leave 3.

So far this is the state of play:

We have 3 left.  This is no 4s, one 2 and one 1.  So 43 = 101011 in binary.

Here is an alternative method:

Start with 43 and divide it by 2 over and over again, writing down the remainder too.  Then carry out the next division, ignoring the previous remainder:

43 ÷ 2 = 21 r 1

21 ÷ 2 = 10 r 1

10 ÷ 2 = 5 r 0

  5 ÷ 2 = 2 r 1

  2 ÷ 2 = 1 r 0

  1 ÷ 2 = 0 r 1

Now look at the remainders in reverse order, which gives you 1, 0, 1, 0, 1, 1.  This, without the commas, is 43 in binary: 101011

Why does this work?

Bonus question: what will the title of the follow-up blog be?