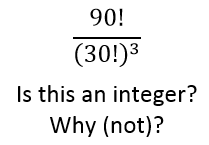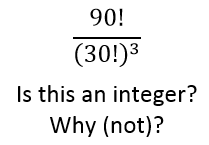Here's part of an article from the Daily Telegraph.  Some questions follow. Don’t hold in a sneeze, warn doctors. It could be the death of you W hen sitting in a quiet theatre or a packed train, stifling a sneeze by holding the nose and closing the mouth may seem like the courteous option. But doctors have warned against the polite practice, after a man ruptured the back of his throat while trying to contain the convulsive explosion of air. Sneezes are powerful, travelling up to 200 mph, according to MIT scientists, with the power to eject debris up to 25 feet. Previously people have been admitted to hospital suffering from burst eardrums, ruptured blood vessels in the eyes, damaged facial nerves, pulled muscles and even cracked ribs from trying to contain the huge force. After seven days the man, who has not been identified, was well enough to be discharged with the advice not to block both nostrils when sneezing in future. Q1) What can we work out? Q2) Wha

Binary is the name given to numbers in base 2.  This means the only digits that can be used are 0 and 1.  We use the powers of 2 as column headings.  Here is an example: This shows 22 in binary, because 16 + 4 + 2 = 22  How can we write 43 in binary?  Try it first before scrolling down (but it is then worth doing so, because there are at least two different ways of doing this!). . . . . . . . . We could start at the left-hand end and see whether we need each number. So:  the biggest power of 2 that fits in 43 is 32.  (We don’t need to worry about 64, 128, 256, etc.) Put a 1 in the 32 column and subtract 32 from 43, leaving 11.  There are no 16s in 11, so put a zero in the 16 column.  There is an 8, so put a 1 in the 8 column and subtract that from 11 to leave 3. So far this is the state of play: We have 3 left.  This is no 4s, one 2 and one 1.  So 43 = 101011 in binary. Here is an alternative method: Start

...but worth thinking about how you can get the answer quickly.  And how many different answers there are. This comes from brilliant.org

Many of the posts so far on this blog have been problems to solve.  This is more of an article to read, but it still involves some opportunities for thought and action. Here are some of the divisibility rules I find useful.  Others may exist too.  Some of these will be familiar to you but I hope there will be something here that will be new to you and that you can make some new connections as well.  Finally, it would be good to be able to prove these rules. (Part 2 will appear at some point and will give some further thoughts on divisibility rules.) These are primary school rules: Divisible by 2: final digit is 0,2,4,6 or 8 Divisible by 10: final digit is 0 Divisible by 5: final digit is 5 or 0 Then there are the rules for 4 and 8: Divisible by 4: final pair of digits forms a 2-digit number that is divisible by 4 Divisible by 8: last three digits form a 3-digit number that is divisible by 8 Hmm.  There is a pattern here.  Divisible by …