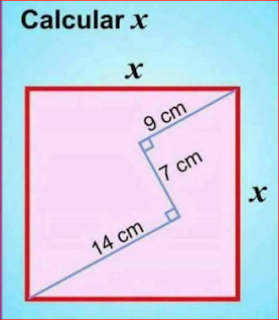
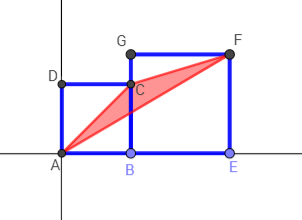
Divisibility Rules (OK) – part 1
Many of the posts so far on this blog have been problems to solve. This is more of an article to read, but it still involves some opportunities for thought and action. Here are some of the divisibility rules I find useful. Others may exist too. Some of these will be familiar to you but I hope there will be something here that will be new to you and that you can make some new connections as well. Finally, it would be good to be able to prove these rules. (Part 2 will appear at some point and will give some further thoughts on divisibility rules.) These are primary school rules: Divisible by 2: final digit is 0,2,4,6 or 8 Divisible by 10: final digit is 0 Divisible by 5: final digit is 5 or 0 Then there are the rules for 4 and 8: Divisible by 4: final pair of digits forms a 2-digit number that is divisible by 4 Divisible by 8: last three digits form a 3-digit number that is divisible by 8 Hmm. There is a pattern here. ...